11.10.3 Unstructured Grid Indexable Elements

Topic Version	1	Published	09/11/2015	Topic Change History
For Standard	RESQML v2.0.1

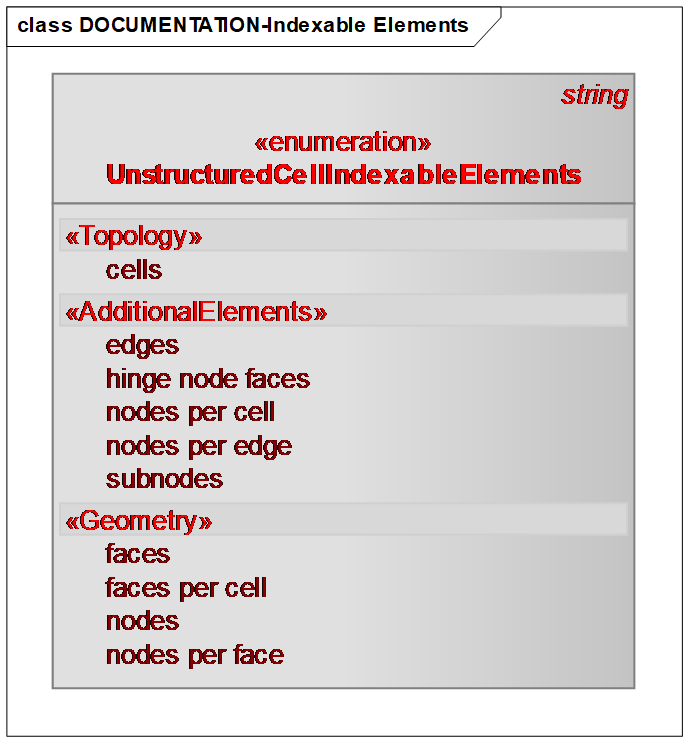
The unstructured grids have the simplest indexing of any of the grid types because all of the topological relationships between the grid elements are explicit. Figure 11.10.3-1 shows the indexable elements organized into three categories: topology, geometry, or additional elements.

Element	Definition/Description of Use
Topology	Those elements whose indexing depends upon the grid index, which in this case is simply the cell count. For an unstructured grid, this index describes the enumeration of the cells of the grid.
Geometry	Those elements that need to be introduced to support the description of the geometry of the grid, which in this case are the nodes on the cell faces. For an unstructured grid, the faces and nodes are indexed according to the face count and the node count respectively. Two other indexable elements are also implicit in the unstructured cell geometry: faces per cell are an ordered list of faces per cell, and nodes per face are an ordered list of nodes per face. Both of these ordered lists are defined implicitly by the RESQML jagged array construction when defining the cell geometry. (For more information about jagged arrays, see 4.3.4 RESQML Jagged Array Construction .)
AdditionalElements	Required to describe higher order geometry or properties. If hinge nodes are used as part of the higher order geometry of the cells, then hinge node faces must be defined. The remaining elements are part of the finite element construction. Edges and nodes per edge need to be specified before edge subnodes can be defined. Similarly, nodes per cell need to be specified before cell subnodes can be defined. Face subnodes require the specification of nodes per face, but their enumeration is already implicit in the construction of the unstructured cell geometry.

Element

Definition/Description of Use

Topology

Those elements whose indexing depends upon the grid index, which in this case is simply the cell count. For an unstructured grid, this index describes the enumeration of the cells of the grid.

Geometry

Those elements that need to be introduced to support the description of the geometry of the grid, which in this case are the nodes on the cell faces. For an unstructured grid, the faces and nodes are indexed according to the face count and the node count respectively.

Two other indexable elements are also implicit in the unstructured cell geometry:

faces per cell are an ordered list of faces per cell, and
nodes per face are an ordered list of nodes per face.

Both of these ordered lists are defined implicitly by the RESQML jagged array construction when defining the cell geometry. (For more information about jagged arrays, see 4.3.4 RESQML Jagged Array Construction .)

AdditionalElements

Required to describe higher order geometry or properties. If hinge nodes are used as part of the higher order geometry of the cells, then hinge node faces must be defined. The remaining elements are part of the finite element construction.

Edges and nodes per edge need to be specified before edge subnodes can be defined.
Similarly, nodes per cell need to be specified before cell subnodes can be defined.
Face subnodes require the specification of nodes per face, but their enumeration is already implicit in the construction of the unstructured cell geometry.

As with the column-layer grids, unstructured grids have a number of “object1 per object2” indexable element kinds, which may be used in favor of “object1” indices when the latter are more complicated. For example, for an unstructured grid, for a cell of the model with N faces as specified by the “faces per cell” element, the faces are numbered from 0 to N-1 in this order. Unlike the faces indexing, which depends upon whether faces are shared between cells, this simple enumeration is completely local to the cell. Faces per cell indices appear in the grid connections representation and the blocked wellbore representation.

Nodes per cell and faces per cell appear as part of the finite element subnode construction, but these should not be confused with the node, face and cell enumerations, each of which have their own indexing.