7.3.4 Z Linear Cubic Splines

There is one interesting variation on the cubic spline in use in our domain: the so-called Z Linear Cubic Spline. As shown in Figure 7.3.4-1 , the resulting interpolant is bounded in Z where a cubic spline need not be.

Figure 7.3.4-1 Z Linear Cubic and cubic splines over two intervals.

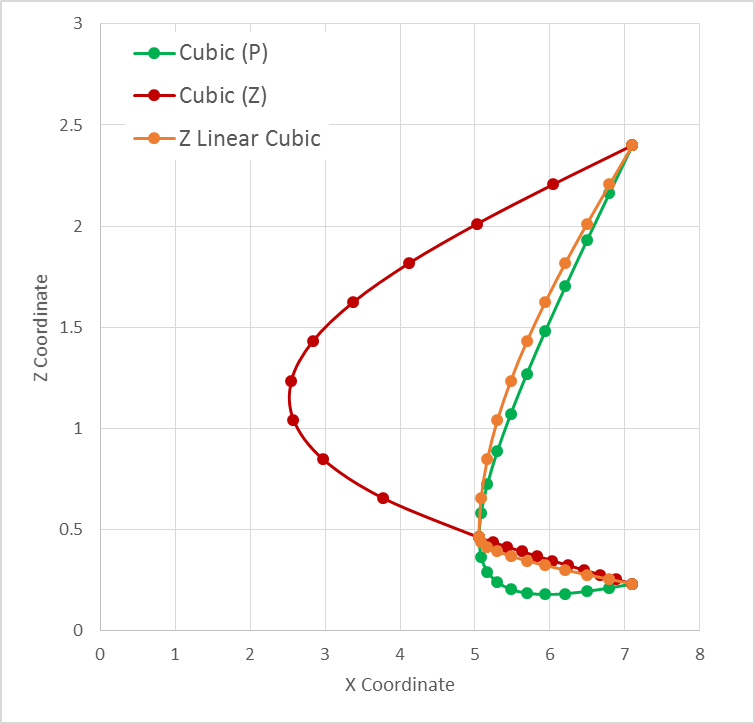
This variation mixes a linear spline interpolant in Z with a natural cubic spline interpolant in (X,Y). It always appears as a natural cubic spline. The figure also include two variations on the cubic splines. The green curve corresponds to the standard natural cubic spline interpolation from Numerical Recipes. The red curve is a cubic spline as a function of the Z coordinate. The Z Linear Cubic Spline is a function of the parameter P, and has continuous derivatives at the knots when expressed as a function of P, but not as a function of Z.