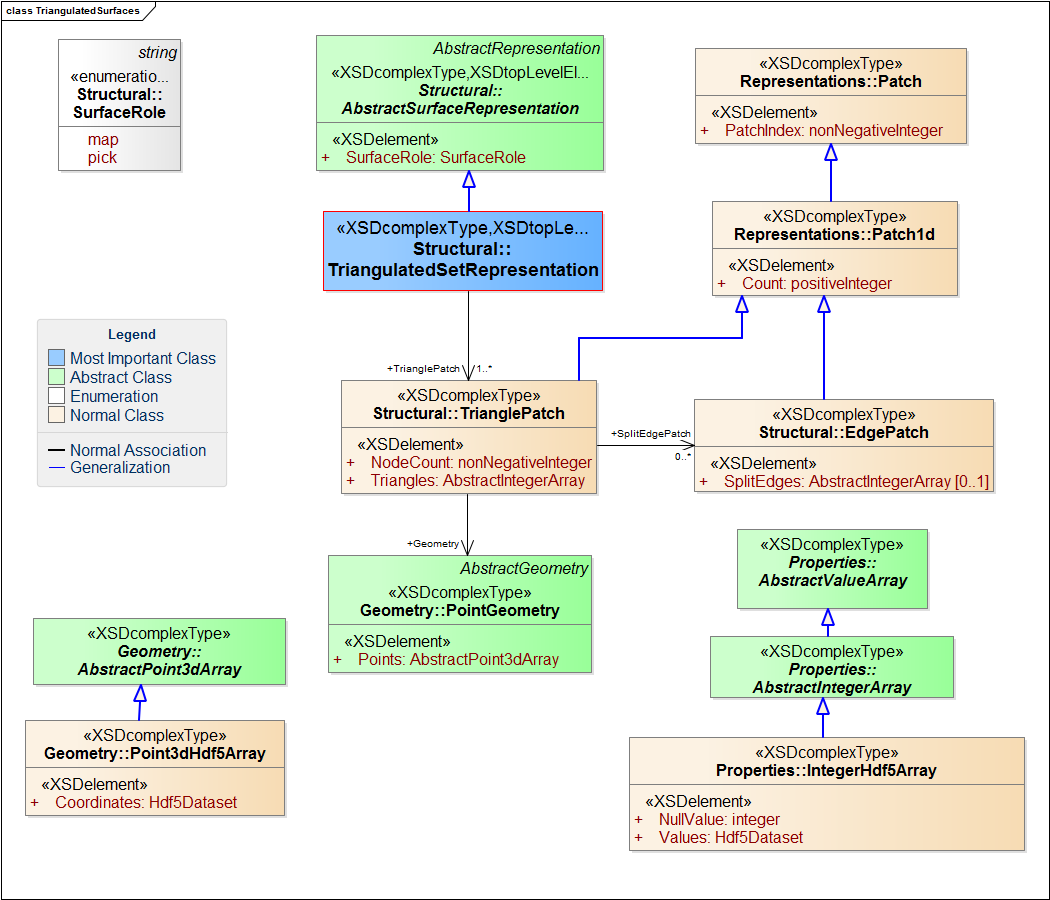
10.2.4.1 Triangulated Set Representations
| Topic Version | 1 | Published | 09/11/2015 | |
| For Standard | RESQML v2.0.1 | |||
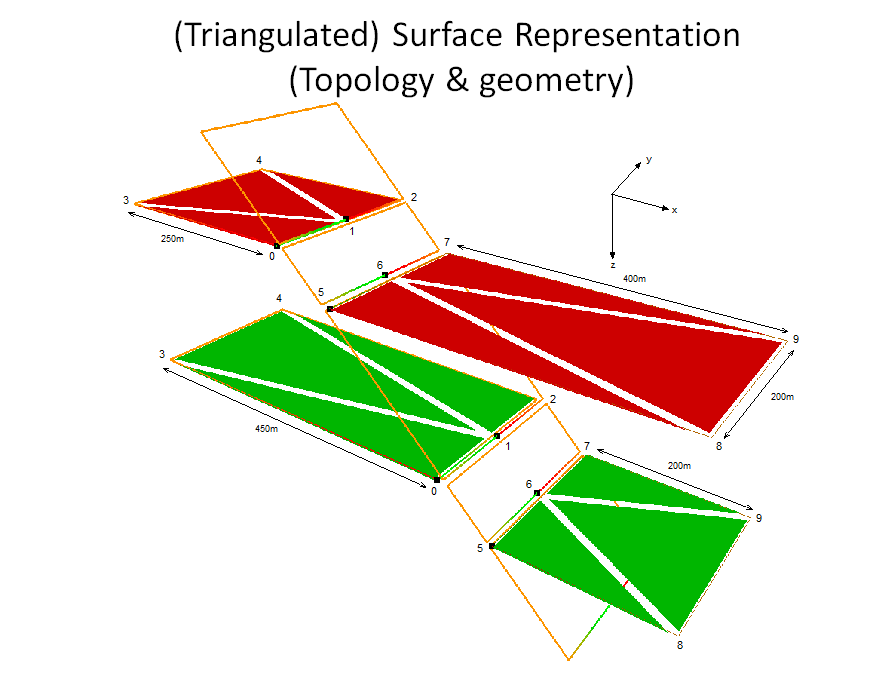
The triangulated set representation contains one-to-many triangle patches (Figure 10.2.4.1-1). (For an example of a triangulated representation that includes geometry and topology, see Figure 10.2.4.1-2 .) The patch 1D count specifies the number of triangles in each triangle patch.
The indices of all the nodes on which the geometry is defined are implicit. For each node, this index corresponds to the order of the nodes in an array of 3D points starting with the first; the array is typically stored in an HDF5 dataset. The topological arrangement of these nodes in triangles is described in triangle patches for each patch in the set.
Triangulated set representations also follow these guidelines:
- Split edges can be indicated in an edge patch instance (to complete the topological arrangement).
- The geometry of the nodes is given by a point 3D array, typically stored in an HDF5 dataset.
- The topology association of the triangles is also typically stored as an HDF5 dataset.
Business Rules. The patch construction is a powerful and important concept in RESQML. For use of patches with triangulated set representations, software writers MUST observer the following business rules.
BUSINESS RULE: Within a patch, all the triangles must be connected.
The patch contains:
- Number of nodes within the triangulation and their locations.
- 2D array describing the topology of the triangles.
BUSINESS RULE: Each triangulated patch must have its proper number of nodes, which are used to set up all the triangles of the patch. If a particular node is shared between two patches, the location of this node must be repeated twice (or more, as used). This case results in two (or more) nodes with two (or more) different indices, but with the same X,Y,Z value.
To express the association of nodes that belongs to several patches, the writer must use the subrepresentation and subrepresentation identity mechanism. (For more information, see 6.3 Patches .)
BUSINESS RULE: The writer must ensure that each patch is non-manifold, that is, where two or more triangles contact at one point (see http://en.wikipedia.org/wiki/Manifold).
BUSINESS RULE: The writer must ensure that a patch is correctly oriented. This means that all the triangles have the same local orientation.