7.3.2 Tangential Cubic Splines

For tangential cubic splines, the control points and the tangential derivativ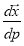es , are specified at each knot. The function is everywhere continuous and differentiable, but the second derivatives may be discontinuous at the knots. Using the cubic functional form within an interval, these four constraints may be used to determine the second derivatives at the interval edges.

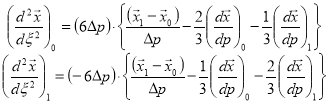
Hence:

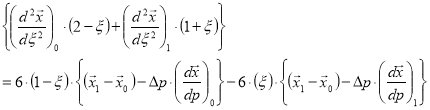
Notice that when written in this form, that zero values for Δp are permitted. This type of spline appears in many interactive graphics packages to provide a smooth interpolant with specified slopes at the knots.