7.3.3 Natural Cubic Splines

For a natural cubic spline, only the control points are specified at each knot. The function is everywhere continuous and differentiable, with continuous second derivatives at the knots. The requirement of a continuous second derivative is sufficient to uniquely define the derivatives. For the edge knots, by definition, the second derivative vanishes. For the internal knots, the second derivative is determined from a quadratic fit through each triple of knots, as shown in Figure 7.3.3-1 .

.

Figure 7.3.3-1 Second derivative at a knot.

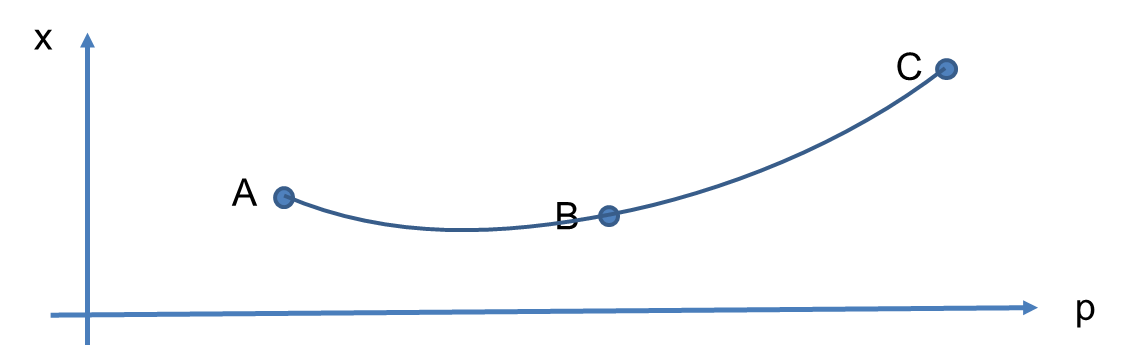
The quadratic functional form that is used in the derivation, and the first and second derivatives at the center knot are as follows.

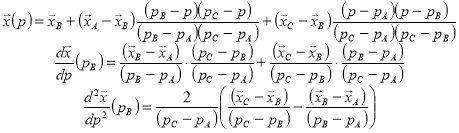
The quadratic fit shows that the best estimate of the slope at the intermediate knot is a weighted average of forward and backward differences, which reduces to a central difference for evenly spaced data. The last of these equations is used in the calculation of the interpolant for the natural cubic spline. Again, care must be taken in their normalization before using the table of basis functions.